Are you a Quiet Speculation member?
If not, now is a perfect time to join up! Our powerful tools, breaking-news analysis, and exclusive Discord channel will make sure you stay up to date and ahead of the curve.
Last week’s article generated a significant amount of positive interactions-–many QS subscribers visited the forums and shared their own investment portfolio. I want to thank everyone who participated in the exercise. Hopefully the experience was an insightful one.
I for one learned something about myself. In the past my bets have generally been conservative in nature. I’ve disclaimed before my hesitation to go deep in an investment because I am eager to reduce risk through diversification. On paper this sounds like a great theory, but it may surprise you to hear that this strategy may not yield the highest possible payout. Diversification is designed to prevent a portfolio from going to zero, not infinity.
Now, my most recent investments have followed a different style to maximize productivity. This new strategy, which I have been implementing informally without realizing, is known as the Kelly Criterion.
Whoa, the Co-Founder of QS is Famous?

Kelly Reid may be famous, but if he is it has nothing to do with the Kelly Criterion. The original theory was developed by J. L. Kelly Jr. in 1956–-I doubt our Kelly is this old.
From Wikipedia, the Kelly Criterion, also known as the Kelly Bet,
“is a formula used to determine the optimal size of a series of bets…The Kelly strategy will do better than any essentially different strategy in the long run.”
The Wikipedia entry goes on to explain that Kelly’s strategy may yield optimal gambling outcomes but there may be individual investing constraints that interfere with obtaining optimal growth rate.
Despite this, I feel the underlying concept should be explored further for potential reapplication to MTG speculation.
Borrowing again from Wikipedia, the Kelly Criterion states:
The equation may look fairly simple, and in reality it does require some assumptions. In MTG speculation, we don't often run the risk of losing everything, but we do risk losing money. The application to MTG finance may be imperfect, but an example is at least worth a try.
A First Test
I’m going to test my Innistrad booster box investment here. Immediately there are some difficult assumptions we must make--this is no exact science.
For the sake of exercise, let’s say I expect Innistrad boxes to hit $200 in a reasonable time frame of a few years. Since boxes can be purchased on eBay for $149 a box, this represents odds of 1.34:1 meaning b = 1.34 ($200 / $149). I feel the probability of earning the $200 is fairly reasonable if we’re willing to wait long enough, so let’s say the probability is 75%. This would make p = 0.75 and q = 0.25.
Plugging in the numbers we get an estimate for what fraction of our portfolio should comprise of Innistrad booster boxes based on our specific assumptions. In this case that fraction equals (0.75 * (1 + 1.34) – 1) / 1.34, or about 56%.
This means that if our assumptions are correct and there’s a 75% chance we will sell at $200 for every Innistrad booster box we purchase at $149, we should take 56% of our MTG funds and place them into this investment. Wow, that’s steep!
Another Example - Shocklands
The example above seems difficult to execute in real life. I don’t have the courage to go that deep on Innistrad boxes. Remember, my current position represents only about 25% of my portfolio. So either I am not 75% confident in making bank or I am not honestly expecting to sell these at $200 per box. One of these assumptions must be incorrect, or else I’m not behaving rationally to maximize profits.
Let me try another example with shocklands, this time comparing scenarios before and after the recent PTQ schedule changes.
Before the change in schedule was announced, Modern season would have lined up perfectly with Standard rotation to drive shockland prices higher. Also, there was not enough time for any reprints and we are fairly confident shocklands aren’t in Theros.
Therefore, let’s assume we were 90% confident in making bank on shocklands with the old PTQ schedule. As for returns, demand would have increased fairly rapidly in the fall, driving prices upward. For this fall, I was expecting to sell my shocklands with a 1.7:1 payout, meaning I would get $12 for every $7 shockland I purchased ($12 / $7 = 1.7).
Applying the equation discussed earlier, I calculate a portfolio fraction of (0.95 * (1.7 + 1) - 1) / 1.7 = 92%! Wow, this would have been incredibly deep! But if we were truly this confident in such a solid return, logic would dictate we should have been this eager to invest.
Even though it seems crazy to invest in anything this deeply, I do want to point out that many QS subscribers did have very significant investments in shocklands.
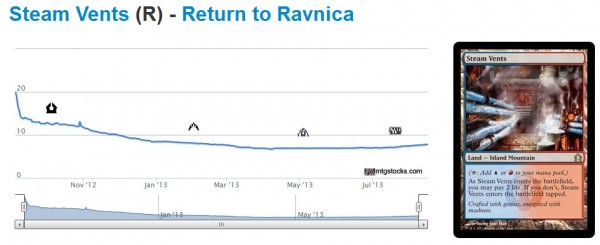
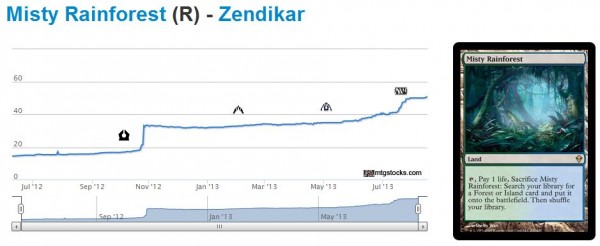
While 92% seems excessive, some application of utility theory may have yielded a more practical number that our emotions could handle. Just look at Zendikar fetchlands, which would have had similar assumptions while they were Standard-playable, and you will see how the Kelly Criterion can yield superior results!
Now let’s test different numbers because Modern season is a year away. Demand won’t be as high and there’s some reprint risk now. I’m actually thinking of selling these this fall anyway once Standard rotates, but I am far less excited about the potential profit. Perhaps I expect $10 now for each $7 shockland, a payout of 1.4:1 ($10 / $7 = 1.4). Also, I am less confident in such a payout so soon after a reprint–-I’ll use a likelihood of 60%.
Now my portfolio fraction is (0.60 * (1.4 + 1) - 1) / 1.4 = 31%. This is a severe drop! With these assumptions, I should invest 31% of my portfolio in shocklands instead of 92%. This is a full 2/3 less the investment!
Can This Really Be Useful?
I don’t have the fortitude to withstand the risk associated with investing 92% of my MTG portfolio in one position. Because of the human aversion to losing everything, I’m guessing I’m not alone in this regard. That’s where Utility Theory and Fractional Kelly Betting come into play–-but that’s an article for another week.
Perhaps the Kelly Criterion can still be useful in a comparative sense, however. The shockland example above illustrates what I mean. With two different sets of criterion, we can use an unemotional, proven strategy to identify where we should make larger bets and where we may need to scale back. Likewise if our assumptions need to change due to a WOTC announcement, a reprint, or a shift in metagame we can use this equation to help us estimate what adjustments are needed.
This tool can also help us sort through the hundred’s of new speculation targets we face each month. If you come across an opportunity that seems risky, consider the likelihood of turning a profit and how much profit, and see how the resulting Kelly Bet would compare versus a more tried-and-true option.
Although I often advocate diversification, sometimes it’s better to just buy another Birthing Pod rather than possibly overpaying on Keen Sense. Of course, if you find Keen Sense or any other cards below mtg.gg buy prices–-well, this equates to 99% likelihood of profit. You should know what to do here, and if it were possible to put 100% of my collection into guaranteed profit I would.
The equation can also help us identify situations where selling is best because it can yield negative numbers! A negative portfolio fraction can be obtained should the payout be too low and unlikely. In this case, we would actually want to sell our entire position (and theoretically, sell short even further if it were possible). Should you end up with this outcome when doing a test, perhaps it’s time to bail and move on.
The Kelly Criterion isn’t the answer--at least not for me. But it is a proven, numerical strategy that is set up to maximize outcome. In the game of MTG there is no guarantee, and we are left with many assumptions on price trajectories. But by putting our best guesses down on paper, the Kelly Criterion can be a valuable tool to help us evaluate if we’re thinking along the right path or if we should move onto the next target.
I cannot bring myself to embrace this tool completely, but I have certainly implemented it lately with extensive investment in Innistrad boxes and shocklands. Now I can finally use numbers to back up my rationale.
…
Sigbits
- I mentioned Elesh Norn, Grand Cenobite recently because the card was sold out at SCG for $9.99 and I expected a price bump. That price bump has happened and now Elesh Norn is $14.99. But she is still sold out! I expect to see $19.99 next.
- Horizon Canopy continues its run--I wish I hadn’t sold mine already! The card is up to $30 on TCG Player and SCG is sold out at $29.99. What interests me is that the foils on SCG are only twice the nonfoils, and there are a couple in stock. If Modern is going to become a mainstay, that multiplier needs to go higher. Especially for a card like Horizon Canopy which is also played in Legacy. Perhaps I will buy these last couple SCG copies…wait let me check the Kelly Criterion…nah, the potential gain is not worth the difficulty moving it given fees.
- Chord of Calling is even stranger. They are selling on SCG’s site for $29.99 but foils are only $49.99. This is a multiplier less than 2x for a major Modern card. I wonder why the multiplier is so low–-if the price bump in Chord is legit, then the foils should at least hit $60 retail to obtain that 2x multiplier.
-Sigmund Ausfresser
@sigfig8






Great article. Though it is heavy on the technical side (as you mentioned on twitter) it does help the casual ‘investor’ to understand when something might be a good bet or not.
Thanks for the comment, Forrest. I recognized the risk I took by writing such a technical article. Is it wrong of me to assume all MTG Speculators are savvy in math and economics? 😉
I still think there’s merit to the approach. The equation may seem intimidating to some, but performing an objective calcualtion can really help a newer MTG investor determine whether or not something is a worthwhile buy. For example, if Keen Sense jumps to $3 each and you can find 12 at $2.50, you can do math to see if there’s enough upside and confidence in the buy to decide if it’s worth trying (versus just buying a foil Shock Land for example). It just adds a level of discipline to buys.
Put another way, if buying a certain card is such a no-brainer, then every other opportunity should be compared with the prospect of just buying more of that certain card.
I’m certainly not an expert at the maths (being a writer and all), but I still enjoyed this.
Thanks for the support, Corbin 🙂
The problem I see in using the Kelly Criterion in an investment setting, is that it only applies (directly) to bets with no alternatives and defined odds.
When there is an option to use a basket of investments, things get significantly more complicated. If we use a basket approach to MTG investing, we want a variety of investments, with each investment having risk associated with different factors.
For an overly simplistic description: We want to invest in cards for control and cards for aggro. The idea is that no matter which is good, we own cards that appreciate in value.
I have liked the perspective you are trying to bring to MTG finance–that of maintaining a variety of assets. Diversification is incredibly important due to the nature of reprints.
Though to be fair, real diversification would have us investing in something other than MTG, as well.
Thanks for adding your thoughts! I am feeling a tug-of-war in my mind right now.
On the one side, you have diversification. It’s very important, it helps reduce risk and ensures you don’t every lose everything. If I go all in on one spec and it gets reprinted or something, I end up losing the farm. This is bad.
On the other side, I have the Kelly Criterion. This is telling me that if I am very confident in a bet and the potential return is high, I should go deep. If I make infinite bets, the Kelly Criterion will eventually yield better results. But there’s a ton more risk here. So I only go deeper on specs if I am very confident I won’t lose everything. If I had done this with Fetch Lands, I would have won multiple farms, if you will.
Applying this criteria is very risky and stressful. I can’t do this optimally, nor should I because it’s not a perfect fit. But the tool provides another way of looking at risk/reward. That was a main reason for the article (plus, I love economics and math). 🙂
I don’t know much about the Kelly equation, but don’t the first two points you made (on Innistrad boxes and shocklands) already contradict each other, assuming that you’re correct on the price goals (and I believe you aren’t that off on those)? You can’t invest 75% of your total funds on something then 92% on something else.
For a simpler counterexample, suppose there are two items, both at $1 now, and one of them is guaranteed $2 in a year, and the other $3. The Kelly equation would tell us to invest 100% in either of the items, which is impossible. This exemplifies what Starwarer mentioned about no alternative odds. After all these thoughts, I think the basic assumption about the Kelly equation is probably that it’s the only investment you make.
You are right in that the percentages don’t work out correctly. But what the Kelly Criterion tells you is that if you have a 1$ bet guaranteed to make you $2, you should go all in. It doesn’t matter if you find another – that’s redundant. You are guaranteed to double up – revel in your wealth 🙂
It is intriguing to consider if you have another bet of $1 guaranteed to make you $100, the fraction is still 100%. So Kelly’s Criterion doesn’t address what to do in this scenario. Then again, if the difference was obvious and each bet was guaranteed, you wouldn’t need some genius from the 50’s telling you what to do. It’d be a no brainer to sell the first bet and move into the second.
Thanks for the engaging comment. I realized when I wrote the article that some of the rationale didn’t apply perfectly, but I thought the topic was thought-provoking enough to write about. Generating this type of dialogue is where much of the value lies. 🙂
Don’t forget that the Kelly Criterion is applicable on bets, meaning all or nothing. Where the outcome is 100% predictable.
So indeed the $1 -> $2 or $1 -> $100 is still a 100% investment, for the simple fact that if you repeat it multiple times, you always will end up in a profitable situation.
To refer to your shock lands fraction of 92% investment (which is when you are 95% confident, not 90% like you mentioned)
If you apply it to the Kelly Criterion there is 95% chance we’ll go from $1 -> $1.70 and 5% that we’ll end up with nothing ($1 -> $0)
The outcome is to invest 92% of available resources (let’s say $1000) in this bet, which is $920 – Once the bet is on, there is
– 95% change our resources grew to $1644 ($80 + $920 x 1.7)
– 5% change our resource dropped to $80 ($80 + $920 x 0.00)
On “average” a $1000 bet will result in 0.95 x 1644 + 0.05 x 80 = 1561.80 + 4 = $1565.80
BUT… MTGfinance is not a “bet” as such and as you mentioned, there are too many assumptions when trying to apply the formula. It’s just a nice measurement to calculate if it feels OK to follow your gut 🙂
Wow, thanks for the thorough follow-up! You’re absolutely right that the Kelly Criterion is for all-or-nothing bets. So the assumption doesn’t fit well with MTG Finance, where there’s a continuum of possible outcomes with possible percent likelihood. This is where Utility Theory will likely be a stronger analysis to consider (but perhaps also more complex).
But you summed up the article perfectly! The calculation is most useful for relative comparisons and to give confidence to your “gut” (or to tell your gut “no”).
uncertainty can be accounted for as losing the bet chance. think margin of error in statistics.
The foil prices you mention seem to indicate that people are still not very willing to foil out their Modern decks, and also the cards in question do not see enough demand in EDH to demand a higher multiplier or maintain their previous multiplier.
It may also be as simple as people having enough of a hard time swallowing paying $30 for a card that was $2 only a couple years ago, and they are just drawing the line with buying the regulars, but unwilling to spend more on the foils. Similar logic could apply with Horizon Canopy, but it’s only price was a little higher.
Yeah, it seems people have not fully made the leap to pay >2x multiplier on some Modern cards. It’s odd how Birthing Pod foils have shot up in price, however. Is that due to EDH?
A good test will be Shock Lands. Many people expect these foils to skyrocket at some point, but this will only happen if Modern players start to demand foils. This in turn will only happen once the Modern format matures so that players can adopt a single deck and play it for years (like in Legacy). I’d hate to pimp out Melira Pod only to have Wizards ban Pod or for some new strategy to become the next best thing 6 months later. Oh, and fear of foil reprints in Modern Masters product also hurts. Time will tell, but there’s definitely opportunity.
yes the Kelly Criterion is useful. it suggest useful strategies for low and high information systems. furthermore, it exposes logical inconsistencies: “I don’t have the courage to go that deep on Innistrad boxes. Remember, my current position represents only about 25% of my portfolio. So either I am not 75% confident in making bank or I am not honestly expecting to sell these at $200 per box. One of these assumptions must be incorrect, or else I’m not behaving rationally to maximize profits.”
in Sig’s case, finding ten similar bets will likely ease his all in fears and still allow Criterion strategy applications.
Mathieu, briilliant add! Thanks for helping me illustrate how the Kelly Criterion can be useful in MTG Speculation! 🙂
Shock Lands, INN Boxes are the two big bets. If I could find 8 more, I likely would feel even better. But I still struggle with the emotional aspect here. At least I recognize my shortcomings, which prevent me from maximizing output.
this is very usefull on mtgo speculation using bulk rares or redemption mythics. Mainly on bulk rares because if the price don’t go up, you probably can’t sell them so it’s like losing everything.
it would be real usefull trying to know what’s the probablility of a bulk and a semi-playable mythic to go up after a price of 0.5 and 1 respectively. i think between 0.8 and 0.9 (probably more on 0.8-0.85).
On more practical way, the function is much more sensible to the probability to happen than to a large profit. if you double the profit but cut the + prob to half, the result is much lower. Summarizing
-You should put big stacks of your budget when the pro is high, even if the profit is low. like 20/30%
-You should spend a small part of the budget, or even none, when the prob is low, even if the reward is very high.
not bad for a bank management. 🙂