Are you a Quiet Speculation member?
If not, now is a perfect time to join up! Our powerful tools, breaking-news analysis, and exclusive Discord channel will make sure you stay up to date and ahead of the curve.
Welcome back readers!
Today's article was inspired by a Facebook trade I did. The cards included in the trade aren't that relevant (as they were for personal use, not speculative gains). What was interesting was that the shipper managed to get more cards in an envelope with a single stamp than I'd seen before. This got me thinking about how many times I have shipped low-end sales in a bubble mailer simply because I thought that I wouldn't be able to get everything into a single envelope.
The cost difference between these two methods is almost $2.50. For sales under $25 that's a cost reduction of 10% or more, which is pretty substantial. If we can use regular envelopes in more cases, it might open up a lot of trades and/or smaller sales that we'd otherwise have to pass on.
Today I'd like to break down the United States Postal Service's requirements to see if we can optimize shipping options for those here in the US. This will obviously be of more relevance to readers living in the States. However, my intent with this article is to show my methodology so that readers in other countries with other requirements can use it to determine their own optimal strategy.
USPS Standard Envelope Requirements
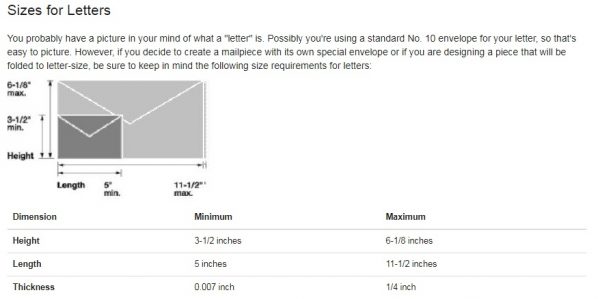
At first glance this looks pretty simple. A nice and short article… Except, as you'd expect from a government entity, there are a whole bunch of additional rules and regulations.
Machinable Requirements
The USPS uses a lot of automation to help sort the millions of mail items they deliver every day (fun fact, I spent some time working on their Flat Parcel Sorting System in my first job out of college; so I can greatly appreciate these automated systems). As is the case with all automated systems, they require more uniform input than a person doing the same thing. Thus there are additional requirements for one's letter-sized mail to run through these systems.
If a letter (or any other package) isn't machinable, it costs extra to ship. We want to make sure all our shipped envelopes satisfy the machinable requirements, which I've copied below.

I realize that looks a bit dry and confusing so I'll break out the key points we want to note. Machinable packages must:
- Be at least 5 inches long and 3-1/2 inches high.
- Be at least 0.007 inches, and no more than 0.25 inches thick.
- Not be of uneven thickness. I'm a bit surprised this isn't defined more in depth with something like a maximum gradient across the envelope. We'll just need to keep it in mind as we may have to add additional packaging to the envelope depending on its size and how many cards we try to fit in it.
- Not exceed a weight of 3.5 oz.
Now that we have our package requirements, let's look at what sizes of commercially available envelopes exist (we don't want to get custom envelopes when commercially available ones cost pennies). We will ignore all that don't meet the requirements listed above.
It was also extremely difficult to find the weight of each envelope type but what I was able to find is that typically most envelopes weigh around 6.75 grams (or 0.24 oz), obviously though the larger envelopes will weigh a bit more and the smaller ones a bit less.
The major dimensions of a typical Magic card are 63mm (2.48in) x 88mm (3.47in), so ideally we want to make sure our envelope size can accommodate that size of object as many times as possible. So here's a table of the most commonly available envelopes. Included are the typical cost per envelope and the maximum number of cards that can fit on one layer.
| Envelope Name | Height (in) | Length (in) | Typical Cost Per | Max Cards per Layer |
| #6 ¼ | 3.5 | 6 | $0.07 | 2 |
| #6 ¾ | 3.625 | 6.5 | $0.06 | 2 |
| #8 5/8 | 3.625 | 8.625 | $0.08 | 3 |
| 4 Bar | 3.625 | 5.125 | $0.12 | 2 |
| #7 | 3.75 | 6.75 | $0.06 | 2 |
| #9 | 3.875 | 8.875 | $0.11 | 3 |
| # 7 3/4-Monarch | 3.875 | 7.5 | $0.08 | 3 |
| #10 | 4.125 | 9.5 | $0.09 | 3 |
| A2 | 4.375 | 5.75 | $0.09 | 2 |
| 5 ½ Bar | 4.375 | 5.75 | $0.16 | 2 |
| #11 | 4.5 | 10.375 | $0.12 | 3 |
| #12 | 4.75 | 11 | $0.10 | 3 |
| A6 | 4.75 | 6.5 | $0.16 | 2 |
| 6 Bar | 4.75 | 6.5 | $0.09 | 2 |
| #14 | 5 | 11.5 | $0.28 | 6 |
| A7 | 5.25 | 7.25 | $0.12 | 2 |
| Lee Bar | 5.25 | 7.25 | $0.26 | 2 |
| A10 | 6 | 9.5 | $0.18 | 4 |
However, that's just the envelope. We also need to consider the thickness of our packaging materials and potentially the card (if it's not embedded in the packaging materials). I checked my typical single-card top-loaders, and they are 0.06 in. on the edges (which tend to be the thickest part). Each top-loader weights around 0.25 oz (found using my kitchen scale) which will be relevant when we look at weight.
We also need to be concerned about overall thickness as well. The thickness of the envelopes on this list should be pretty uniform (though paper stock may have some slight bearing on it) and most envelopes will be around 0.008 inches thick.
The other packaging material we might want to look at is your typical cereal box cardboard which can be used to create a makeshift top-loader with varying thickness (based on how many cards are inside). If you mail cards and the only protection is from cereal box cardboard they may get bent up or damaged in transit, so I don't personally recommend them. But if you do use them, I discuss the calculations for that method below.
This cardboard is typically 0.01 inches thick. The weight of a rectangle slightly larger than a card is around 0.1 - 0.15 oz. Corrugated cardboard, which provides more support, is much thicker and can range a great deal.
A Magic card itself tends to weigh around 0.06 ounces (1.8 grams).
Optimization
So we have our list of max requirements courtesy of the USPS and we also have the necessary information regarding our packaging materials and the Magic cards themselves. Let's put all that together to see what the optimal packaging options are.
For Top-Loader Protected Packages
Let's define our variables to make sure everything is easy to read.
- M = Maximum number of top-loaders that will fit in a package
- L = Maximum number of top-loaders that will fit on one "layer" of an envelope
- T = Maximum thickness of the package (0.25 in)
- E = Envelope thickness (0.008 in)
- A = Top-loader thickness (0.06 in)
- W = Maximum package weight (3.5 oz)
- V = Envelope weight (0.125 oz)
- P = Top-loader weight (0.25 oz)
- C = Card weight (0.06 oz)
- X = Number of cards per top-loader
The first step was determining how many top-loaders I could fit into the envelope without exceeding the thickness for each option. I did this with the following equation.
![]()
The l-shaped brackets are the mathematical symbol for rounding down to the nearest integer. You'll notice these appearing in lots of the equations below. This is important because we can't have fractions of cards/top-loaders/envelopes, and we want to play it on the safe side.
This gives you the theoretical maximum number of top-loaders you could fit into the various envelopes. If you then multiply by the number of Magic cards you can fit per top-loader (either 2 or 3), you can calculate the maximum number of Magic cards that could safely fit into an envelope.
Volume isn't our only requirement; we also have to be concerned about weight. To calculate the maximum allowable weight we use the following equation.
![]()
Again we round down because we can't go over. This allows an absolute maximum of eight top-loaders in an envelope.
We can now compare our two limitations and see that they both set a maximum of eight top-loaders per envelope (assuming 2 cards per top loader). That means we can ship up to 16 cards per envelope per the USPS volumetric and weight guidelines.
Unfortunately, there are additional guidelines we want to consider, specifically with regards to "uneven thickness." This means that our top-loader layers need to have an even number of top-loaders per layer. Any envelope with 3 top-loaders per layer would result in two layers with 3 top-loaders and one with 2 (to avoid going over the weight maximum of 8) which would then have an uneven thickness.
Ultimately, this means that our envelop options here in the US are likely the following:
- #6 ¼
- #6 ¾
- 4 Bar
- #7
- A2
- 5 ½ Bar
- A6
- 6 Bar
- A7
- Lee Bar
- A10
The A10 envelope can actually allow a full four top-loaders per layer, which would keep your envelope thickness down. However, the biggest problem with this is that they cost about 2.5-3 times as much as other envelopes and may have issues with smaller numbers of cards.
It might count as uneven if you only send one top-loader with 1-2 cards in it, so that is something to consider. The best solution is probably to give yourself options on envelopes, and keep some of the smaller ones as well as some A10s for orders with larger numbers of cheap cards.
For Cardboard Protected Packages
For this set of equations we will use some of the previously defined variables as well as the following new variables:
- B = Cardboard thickness (0.01 in)
- R = Card thickness (0.012 in)
- A = Weight of cardboard (0.125 oz)
- D = Maximum number of cards per envelope thickness
- E = Maximum number of cards per envelope weight
While I want to reassert that I don't really recommend this option (it doesn't protect the cards nearly as well as a top-loader) if you're doing a $5-$10 trade that consists of a lot of cheap cards you may be willing to risk it. As I said earlier, the biggest benefit to this route is that many cardboard options are cheaper than top-loaders. You can make your own by sandwiching two pieces of cardboard around the cards your sending. The cardboard is thinner than top-loaders and could allow you to fit a few extra cards into the envelope.
For this optimization we still want to use the same results for L (max number of top-loaders in one layer). We won't actually be using top-loaders, however, the 2D dimensions for our cardboard end pieces should be similar in size so the number per layer should remain the same.
So for this we calculate the maximum thickness allowable for one of these sandwiches with the following equation. If you want to use thicker cardboard (and thus reduce your risk of damaging the product in the mail) you can include that and recalculate all these numbers.
![]()
We can then take that number and multiply it by L to determine the maximum number of Magic cards one could fit into the envelope.
But just like with the top-loaders, this is only one of the necessary equations because it too assumes that there is no "max weight" requirement. If we now want to look at the maximum allowable weight, we calculate using this equation (which again is influenced by the cardboard chosen).
![]()
Filling in these variables I see that the maximum number of cards per envelope with only a maximum weight requirement is 46.
So when we compare our two equations we see that the package thickness is actually where we are restricted first (as we are limited to 18 cards via the thickness requirement), which means that the actual maximum number of cards we can fit into an envelope with cereal box protection is 36 cards. Doing so puts our envelope weight at 2.9 oz. which gives us a bit of a safety net with regards to the max weight requirement.
Conclusion
The point behind this article was to review the standard USPS package requirements that allow for a single stamp in order to reduce shipping costs and possibly open up new avenues of lower-cost trades or sales because of this reduced cost. That being said, I would still be weary of trying to ship a large a number of cards in a standard envelope because I know how finicky automated sorting machines can be.
I also realize there are a significant number of other options when it comes to the variables I've chosen. For example, they make four-card top-loaders that can actually hold 5-7 cards, but are thicker than the ones I used in my calculations above.
When I started this article I didn't realize just how many factors there were to consider, nor did I expect that one might be able to ship so many cards via a plain white envelope. I would love to know the highest number of cards any of you have shipped with a plain white envelope and single stamp, as empirical data would be more accurate than these theoretical calculations.





In my experience, USPS favorably rounds the weight of envelopes, because it just makes everything easier from their perspective, wouldn’t be worth the time to bust people’s balls over fractions of ounces. That means you can send a 3.4oz envelope by simply applying two extra oz stamps with a regular stamp. You can also send a 1.4oz envelope without adding any extra postage, and it’s easy to have them check the weights if you go to the post office in person. I typically send everything non-machinable too because it’s a small price to pay for the cards to be safer.