Welcome back, readers! I'll be upfront: this week's article will most likely appeal mainly to those with very large trade collections and stores. However, it is one I haven't seen anyone specifically focus on and is definitely a subject with a lot of real-world financial implications.

The subject is inventory management. Managing one's inventory well will save you a lot of money over time and it can also help make you money. While it's important to have a good selection of cards in order to have what customers want immediately available, it's just as important not to sink too much money into inventory that can't move.

This is a very easy trap to fall into. As a store it can be easy to acquire inventory if you buy aggressively, but inventory that doesn't sell ties up money that may be needed for other store functions (rent, employee salaries, utilities, etc.). After all, landlords and grocery stores don't accept Magic cards as payment.

This is a pretty big topic, so I'm splitting into two articles. Today we will be focusing on dead stock and one way of calculating the amount of any specific card you should keep in inventory.

The Danger of Dead Stock

Dead stock is the name given to merchandise that has little to no demand, and is thus almost unsellable. The best examples of this type of stock are cards whose value was solely tied to Standard and which haven't seen any relevant eternal play. Cards like Boon Satyr, that often held price tags in the $2-$4 range, but after rotation sit at bulk levels.

While it can be difficult to determine which cards will fall into this category, there are a few indicators one can look for before the price bottoms out and the cards get moved into the bulk category.

1. Have your casual customers been looking for them periodically? If so, then there may be some appeal after rotation and you may be able to move a small number of them to these players. This is especially true of cards that are tied to "casual" styles of play: mill, tribal, lifegain, tokens. That is by no means the full list of casual-interest cards, but we often see casual groups having specific preferences and one must be in tune with those preferences to get a true feel for this potential.
2. Does the card get better with multiple opponents? This is obviously relevant with Commander or multiplayer formats (something like the Primordial cycle from Gatecrash).
3. Was the card featured in "fun" Standard decks? While I accept that the definition for fun will vary greatly, the point here is that it's not uncommon for some kitchen-table players to want to build the best Standard decks of yesteryear, often adding cards that weren't legal at the time. I can certainly recall doing exactly this when Tempest block rotated out (I built RecSur) and then again when Urza block rotated out (I built Academy). At the time I didn't have the funds—I was a middle school/high school kid with no job—to buy or trade for these powerful decks while they were Standard-legal, but when they rotated out the prices dropped out on many of the cards. This was before eternal formats were really popular, but budget-conscious players are still doing this today.

Now it's important to keep in mind that your local playerbase will heavily dictate demand of cards. If you have a robust local playerbase (i.e. plenty of competitive and casual players), you likely need to maintain some sort of minimal stock of Standard-only cards, even knowing that they will likely become dead stock at rotation, in order to appease the competitive crowd.

However, if you can identify these cards far enough in advance of rotation, you can make sure that you reduce your stock levels in preparation of the shift from in-demand to dead stock. Fortunately, there are actual equations we can use to help us with this.

Calculating Optimal Order Quantity

Optimal Order Quantity is the amount of product one should order, based on several variables, in order to balance the risk of dead stock and shortages. This figure can be calculated if you know the costs of holding, shortages, and the demand you're trying to meet.

I'll preface with a caveat about calculating demand. In the equation we're using, demand refers to an established quantity, or known demand. Typically this refers to companies who have specific customers who consistently re-order the same products. Say, for example, a newspaper company that needs to buy a lot of paper.

They will likely buy around the same amount of paper monthly from the same supplier. These suppliers can then factor in that known demand into their equations for inventory control.

In Magic finance, known demand is more ambiguous. We'll cover that more below.

First, the equation:

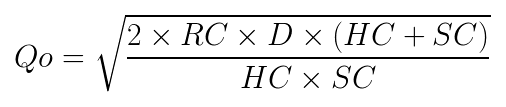
where:

• Qo = Optimal Order Quantity
• RC = Reorder Cost (in our case the buylist price)
• D = Demand
• HC = Holding Cost (value lost while holding a Standard card with deteriorating value)
• SC = Shortage Cost (value of lost sales and unhappy customers)

Unfortunately, the real world isn't like text books where all the variables are known, so we may have to calculate or estimate some of these variables as well. Obviously our final Optimal Order Quantity value will be influenced by these calculations/estimations.

Holding Cost

To calculate HC (Holding Cost), I would suggest looking at a card's current value, how many months it has left in Standard, and its expected value post-rotation (likely near bulk, or retail of $0.5 - $1.0). This should lead us to developing a sort of deterioration rate for the price. This rate should be an average of the deterioration rates of Standard-only staples, i.e. cards whose demand is principally determined by Standard play. Ideally we would want to pull this number from numerous Standard rotations to create the largest blanket possible.

To do this, I gathered 20 cards that were Standard staples, but which currently see little to no eternal play. I then looked at the amount of value they lost each month leading up to rotation and took an average. Here was my sample:

What I found is that on average these cards drop about 9% per month leading up to rotation, starting around the six-month mark. (Interestingly enough, there were many positive gains seven and eight months out, and the negative trend only started at six.)

Obviously, shifts in the metagame will cause some to spike further, and those that fall out of favor might drop considerably more during that window, but overall we're seeing close to a 9% drop. This number could of course be refined further with additional data points, if you were so inclined.

Assuming this 9% loss, we can calculate the Depreciated Value (DV) over any number of months like so:

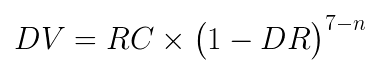
In this equation n is the number of months before rotation. We want to start measuring from the sixth month out, when depreciation begins—hence the (7 - n) term. Depreciation Rate (DR) is the 9% figure we estimated above, but could be replaced with whatever you've calculated as the monthly loss.

Dividing this Depreciated Value into the Reorder Cost (RC) gives us the Holding Cost (HC). Altogether, here's what the full formula looks like (The RC in the numerator and denominator actually cancel each other out):

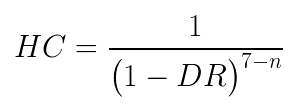
This gives you a good idea of what the holding cost could be, but it isn't exact. In researching for this article I was not able to find any definitive equation to determine holding cost. It seems that in many cases there are so many variables that holding cost is calculated on a per-need basis by each company. However, using this equation I did get results that made logical sense, specifically that as you get nearer to rotation your Optimal Order Quantity gets closer and closer to your known demand.

Shortage Cost

Next we need to determine the Shortage Cost (SC), which is the cost of not having the product in stock. The reason I picked this version of the equation is that it's not uncommon for smaller stores to run into shortages of Magic singles, as the cost of keeping a fully stocked inventory is too high for many stores.

When it comes to many larger companies, shortage cost can be understood as something like a "fine" imposed by their customer if they fail to supply product by the stipulated time. Of course, it works differently for local game stores—shortage costs may be a loss of a perspective sale (best case) or of a customer (worst case). Unfortunately, these two options are dramatically different regarding damage to the business, and are difficult to calculate.

For the sake of this calculation let's assume that the store only loses perspective sales (as opposed to customers). For the most accurate picture, it would be ideal for a store owner to keep track of the times an order was unable to be filled due to lack of product. Then you would sum up the value of all these "lost sales," and divide by total sales for a given time period.

So for our example we will assume that a store owner missed out on $100 in sales over $1000 in sales per month. This would equate to a shortage loss of $0.10/dollar (or units of dollar per dollar). In order to calculate our shortage cost it would be best to multiple our 0.1 by the retail price of the card we are reviewing.

Demand

Last but not least we have our Demand (D). As stated, this whole set of equations stems from a known demand, which I think we can all agree when it comes to Magic cards is likely not all that known.

However, for the sake of argument let's say your store has three players that are ultra competitive and will always buy a playset of any given "hot staple" if it shows up in a Top 8 deck. This means you will sell at least 12 copies of any given hot Standard staple if it's competitive. We also have to assume they don't have any copies (though if you knew how many they had you could subtract it from 12 and change that to your known demand).

Conclusion

Next week I will continue on this subject and cover Unknown Demand (which is a much more complicated set of equations). Hopefully though, this topic has caused readers to really think about their inventory and look at it from a more logical (and scientific) angle as opposed to "gut feeling" or guesstimates.

If we have any logistics specialists or people who work a lot with procurement or inventories, I would especially love to hear your thoughts on this topic in the comments below. I will be the first to admit that I didn't realize how in depth I would need to go to tackle this particular subject.

While I'm very good at math, my engineering background makes me bristle at some of the ambiguity behind these types of equations. I'd rather have one massive equation that I could eliminate variables from than to have to determine what variables I want to use in my equation. As I was unable to find anything like this (despite a good bit of searching), I was forced to go down certain paths. I did discuss this with my girlfriend, who has an MBA, and she did agree with my reasoning, but feel free to challenge me on it.